连载丨热成像和超声结合表征混凝土表面下的裂缝（2）

2.3 数值模拟

为了对比不同量级裂缝深度的不同影响，进行了数值模拟。其工作原理是基于有限差分法求解二维弹性波动方程。本文认为钢纤维混凝土材料是弹性的，没有粘性成分。其拉梅常数λ=12 GPa，μ=16.5 GPa，密度为2 400 kg/m³，纵向速度为4 300 m/s，弹性模量为40 GPa，泊松比为0.2。本文数值模拟建立的模型的几何形状为矩形，厚度为100 mm，与试验试件相似。计算的网格尺寸设置为0.2 mm×0.2 mm，远小于43 mm的纵向波长。为了缩短计算时间，试件的长度减小到200 mm，对两侧施加无限边界条件，消除来自边缘的影响。两个模拟传感器长15 mm，与实际的传感器相似，并放置在试件顶部，间隔70 mm。传感器计算了其定义长度上的平均横向位移。模拟案例涉及无裂缝几何形状以及具有裂缝的几何形状。表面和裂缝之间的完整层（裂缝深度）变化分别为60 mm、40 mm、20 mm、10 mm、8 mm、5 mm、3 mm和1 mm。裂缝的厚度为1 mm。

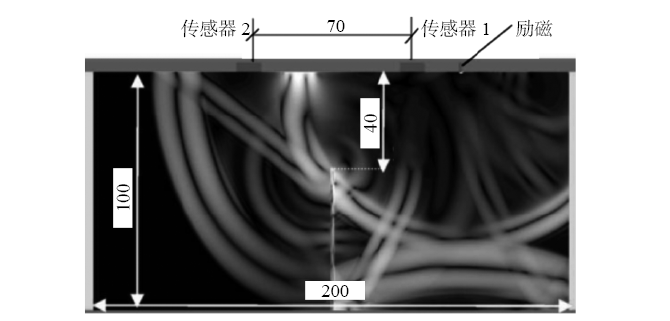
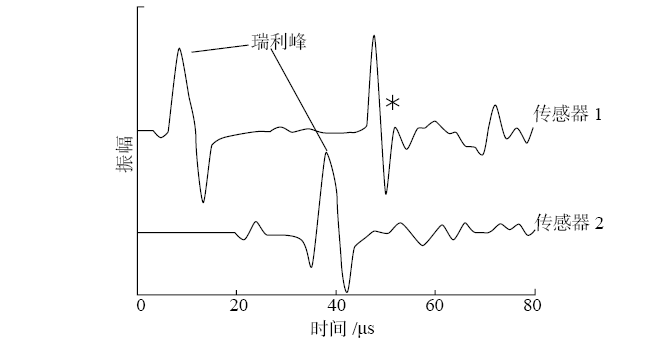
图7（a）为地表以下40 mm处存在裂缝的试件的位移场快照，其时间点对应于100 kHz波的一个周期激励后的32 μs。图7（b）显示了本案例模拟后获得的波形。观察传感器2的情况可以发现，在瑞利周期之前可以清楚地看到瑞利波初始纵向到达后，有足够长的路径可以按照不同的速度分离出不同的模式。传感器1记录的第二个强周期（用“*”标记）是来自光束底侧的纵波反射。

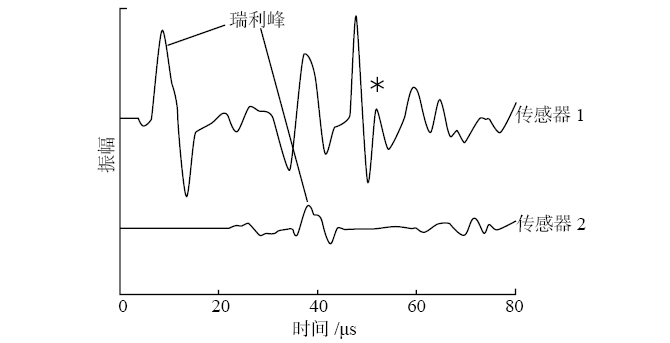
图7（c）为地表以下1 mm处存在裂缝的试件的位移场快照，对应的波形如图7（d）所示。由于裂缝靠近表面，只有少量能量可以向传感器2传播。位移场被扭曲，传感器2的波形振幅要低得多，这是因为大部分能量被不连续地反射回来。在任何情况下，瑞利波对传感器和速度测量的贡献都是明确的。在传感器1的响应上再次看到纵向反射，以及之前在大约40 μs处的另一个强循环，这是瑞利波在裂缝上的反射。由于裂缝的深度足以使大多数的能量扩散出去，因此在图7（b）中没有发生纵向反射。

（a）

（b）

（c）

（d）

图7 地表以下40 mm处和1 mm处存在裂缝的试件的位移场快照以及模拟得到的相应波形

（a）地表以下40 mm处存在裂缝的试件的位移场快照；

（b）40 mm处的波形；（c）地表以下1 mm处存在裂缝的试件的位移场快照；（d）1 mm处的波形

为了研究波长的影响，改变瑞利波的频率，分别为100 kHz、200 kHz和20 kHz，相应的瑞利波波长分别为23.2 mm、11.6 mm和116.2 mm。图8为声音材料对传感器2的波形振幅进行归一化后，不同裂缝深度下传感器2的波形振幅。随着裂缝深度的减小，测得的波形振幅快速下降，当裂缝深度为0 mm时，测得的振幅降低到瑞利波归一化振幅的20 %。随着地表以下裂缝深度增加，100 kHz和200 kHz的瑞利波的振幅基本不随裂缝深度的增加而增大，这意味着100 kHz和200 kHz的瑞利波对深度超过20 mm的裂缝失去了敏感性。

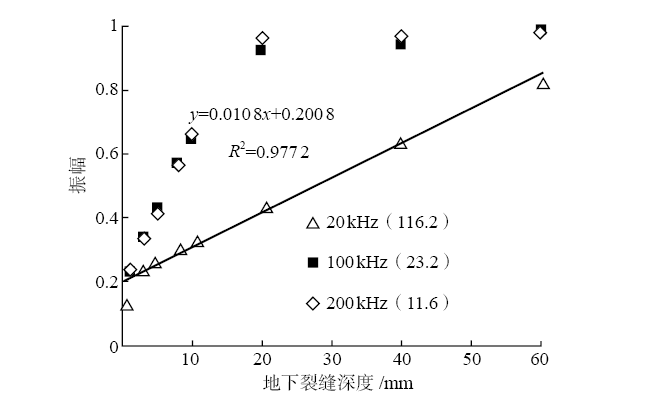
图8 地下裂缝的振幅与深度

然而，当裂缝深度从0 mm增长到60 mm时，20 kHz的瑞利波的振幅的增长速度缓慢，与深度呈现正相关关系。这与试验测量结果一致，试验测量结果表明，波的振幅是对潜在损伤最敏感的参数。本文没有对更深的情况进行模拟，因为更深的裂缝源于埋在地表以下50~60 mm的金属钢筋。总之，对于具体的混凝土表面以下缺陷，一些参数（如深度）可以采用单侧波法进行表征。然而，大型结构的裂缝并不总是能够被观察到的，因此，为了确定裂缝的位置，进而确定超声传感器的安装位置，必须找到一种能够进行裂缝初定位的方式，本文采用红外热成像技术。

2.4 红外热成像技术

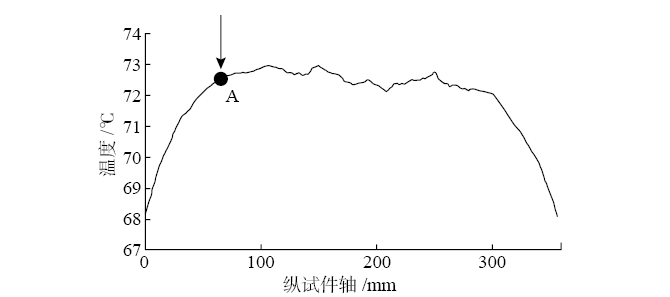
图9（a）显示了完整试件的温度图。当试件边缘附近加速冷却时，试件中心的温度场是均匀的。为了提高检测的准确性，将扫描区域划分为1.5 mm×1.5 mm的网格，每根垂直线上有50个关键节点。混凝土通常有一些可见的表面缺陷（如气泡），其可以作为温度释放点。因此，它们也被红外摄像机捕捉到，可能会误导表征。为了减少这种误导，计算了网格每条垂直线上节点的平均温度。像气泡这样的小表面缺陷只能改变局部几个节点的温度读数。但是，这些被改变温度读数的节点不会影响50个关键节点的温度平均值。声音样本的平均温度线如图9（b）所示。例如，特定点（如图9（b）中的A）即图9（a）中相应垂直粗线中包含的所有节点的温度平均值。

（a）

（b）

图9 试件温度图及试件轴线平均温度示意

（a）完整试件的温度图；（b）试件轴线的平均温度

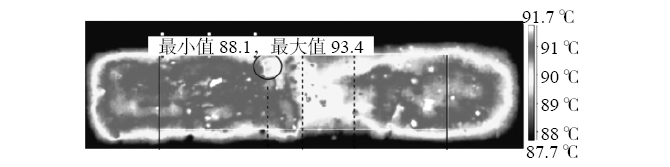
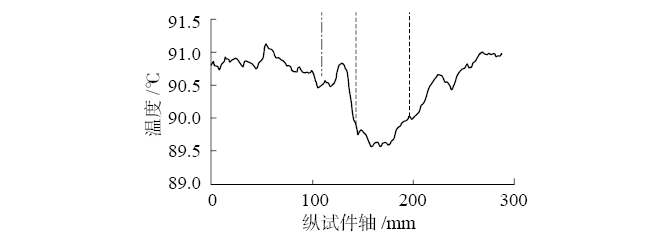
图10（a）显示了混凝土表面以下有裂缝试件的温度图，缺陷区域内的温度场变化较大。图10（a）表明了混凝土表面下方的裂缝区域，这一点可以通过图10（b）的平均温度曲线得到证实，其清楚地显示了150~190 mm区域内温度最低，这个区域是实际情况下需要用超声波传感器检查的区域。值得一提的是，如图10（a）中圆圈所示，在某些位置，由于小的表面异常，温度与缺陷顶部的温度相似。然而，这些小的表面异常在温度曲线上产生了适度的局部最小值，因此无法“掩盖”缺陷区域的特征。图10（c）显示了特定试件的侧视图。裂缝向上部分裂，增加了异常，有利于红外辐射表征，且裂缝尖端在混凝土表面以下约4 mm处。

（a）

（b）

（c）

图10 跨中挠度为2 mm时的测试图

（a）试件温度图；（b）试件轴线的平均温度；（c）试件侧视图

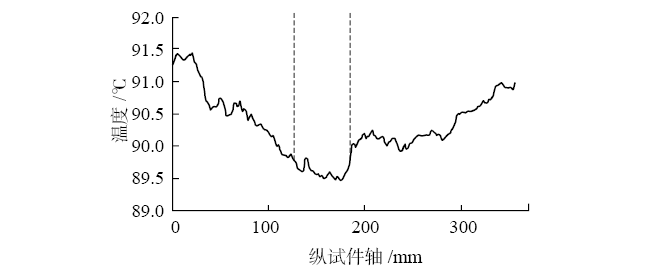
图11（a）显示了试件在跨中挠度为1.5 mm时产生的裂缝的温度图。试件中心附近的较低温度场在热成像仪中再次可见，图11（b）的曲线再次显示了一个清晰的最小值，表明通过超声检查复杂区域是可行的，裂缝在混凝土表面下方约8 mm（图11（c））。

（a）

（b）

（c）

图11 跨中挠度为1.5 mm时的测试图

（a）试件温度图；（b）试件轴线的平均温度；

（c）试件侧视图

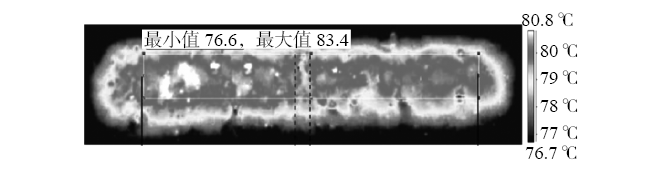
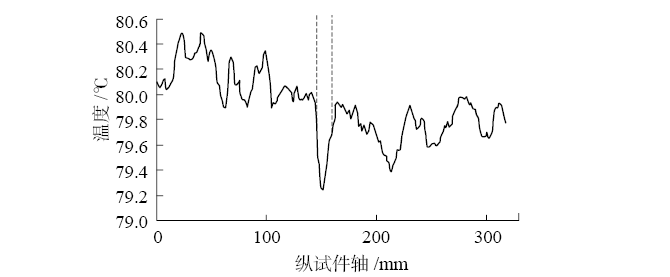
图12涉及最小的裂缝，对应1 mm的跨中挠度。这种情况下温度场不清楚，因为混凝土表面下缺陷造成的异常小于1 ℃，如图12（a）所示。在同一范围内还有其他几个波动，由于表面缺陷，用肉眼检查热像仪可能会导致不同的可疑点。在这种情况下，缺陷部位存在显著的局部极小值（图12（b）），因此，通过局部极小值两侧曲线找中线的方法来确定裂缝顶端位置是一种有效的方法，该方法在150 mm处的最小值与裂缝顶端的位置相对应。

如图12（c）所示，裂缝尖端在混凝土表面以下约11 mm处。如果观察到另一个强烈的温度最小值，如图12（b）中的210 mm最小值，安全起见，可以用超声波对具体位置进行扫描。若无裂缝，则不会测出干扰波。

（a）

（b）

（c）

图12 跨中挠度为1 mm时的测试图

（a）试件温度图；（b）试件轴线的平均温度；（c）试件侧视图

3 结束语

本研究通过两种无损检测技术扫描钢纤维混凝土试件，以识别4点弯曲产生的地下裂缝。首先使用热成像技术扫描被检查区域，再使用单侧超声测量来更详细地表征裂缝深度，并对具体的弹性波问题进行了数值模拟。结果表明，表征性能最强的是波的振幅，在试验和模拟中，瑞利波振幅随裂缝深度的减小而下降，下降程度超过80 %，而低频率（20 kHz）的瑞利波对隐藏在地表之下的裂缝的深度变化更加敏感。

为了确定波形参数与裂缝深度的关系，需要进一步的研究。就热成像而言，研究结果是令人振奋的，因为在实验室温度较高的环境中，可以用热像仪或沿样品轴的平均温度曲线来识别表面缺陷，但仍需在低温下进行进一步的鉴别，以证明其在实际应用中的适应性。

（本文已完结。）